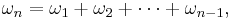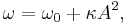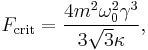Nonlinear resonance

In physics, nonlinear resonance is the occurrence of resonance in a nonlinear system. In nonlinear resonance the system behaviour – resonance frequencies and modes – depends on the amplitude of the oscillations, while for linear systems this is independent of amplitude.

1 Description
2 Nonlinear resonance shift
3 See also
4 Notes and references
- 4.1 Notes
- 4.2 References
5 External links

Description

Generically two types of resonances have to be distinguished – linear and nonlinear. From the physical point of view, they are defined by the fact whether or not external force coincides with the eigen-frequency of the system or not (linear and nonlinear resonance correspondingly). The frequency condition of nonlinear resonance reads

$\omega_n=\omega_{1}%2B \omega_{2}%2B \cdots %2B \omega_{n-1},$

with possibly different 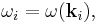$\omega_i=\omega(\mathbf{k}_i),$ being eigen-frequencies of the linear part of some nonlinear partial differential equation. Here 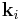$\mathbf{k}_i$ is a vector with the integer subscripts $i$ being indexes into Fourier harmonics – or eigenmodes – see Fourier series. Accordingly, the frequency resonance condition is equivalent to a Diophantine equation with many unknowns. The problem of finding their solutions is equivalent to the Hilbert's tenth problem that is proven to be algorithmically unsolvable.

Main notions and results of the theory of nonlinear resonances are:^[1]

The use of the special form of dispersion functions 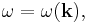$\omega=\omega(\mathbf{k}),$ appearing in various physical applications allows to find the solutions of frequency resonance condition.
The set of resonances for given dispersion function and the form of resonance conditions is partitioned into non-intersecting resonance clusters; dynamics of each cluster can be studied independently (at the appropriate time-scale).
Each resonance cluster can be represented by its NR-diagram which is a plane graph of the special structure. This representation allows to reconstruct uniquely 3a) dynamical system describing time-dependent behavior of the cluster, and 3b) the set of its polynomial conservation laws which are generalization of Manley–Rowe constants of motion for the simplest clusters (triads and quartets)
Dynamical systems describing some types of the clusters can be solved analytically.
These theoretical results can be used directly for describing real-life physical phenomena (e.g. intraseasonal oscillations in the Earth's atmosphere) or various wave turbulent regimes in the theory of wave turbulence.

Nonlinear resonance shift

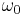Nonlinear effects may significantly modify the shape of the resonance curves of harmonic oscillators. First of all, the resonance frequency $\omega$ is shifted from its "natural" value $\omega_0$ according to the formula

$\omega=\omega_0%2B\kappa A^2,$

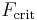where $A$ is the oscillation amplitude and $\kappa$ is a constant defined by the anharmonic coefficients. Second, the shape of the resonance curve is distorted (foldover effect). When the amplitude of the (sinusoidal) external force $F$ reaches a critical value $F_\mathrm{crit}$ instabilities appear. The critical value is given by the formula

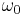$F_\mathrm{crit}=\frac{4 m^2\omega_0^2\gamma^3}{3\sqrt{3}\kappa},$

where $m$ is the oscillator mass and $\gamma$ is the damping coefficient. Furthermore, new resonances appear in which oscillations of frequency close to $\omega_0$ are excited by an external force with frequency quite different from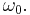 $\omega_0.$